Soon, after writing my first meta programs with C++ templates, i realized, that certain programming patterns lead to sky rocketing compile times. I came up with rules of thumb like “Prefer pattern matching over if_else_t”, and “Prefer nested type lists over variadic type lists”. But i did not know how much faster which pattern is, i just knew about tendencies. Finally, i sat down to write some compile time benchmarks, and this blog posts presents the results.

Creating Lists

A fundamental thing to measure are lists. Everything else which can grow to arbitrary sizes, will somehow be implemented using lists. There are different possible ways to implement lists. I present measurements of nested and variadic type lists. This article does not explain how to implement them, but there is an article about C++ template type lists already.

The first benchmark just creates lists of rising sizes, and measures how much time that takes. The lists are generated from integer sequences, just like those from this article which explains how to generate integer sequences at compile time.

I present graphs for doing this inside Metashell, and also using real compilers. Metashell is a great tool for debugging meta programs, or playing around with expressions. It is basically what ghci is to Haskell, an interactive shell for programming.

Since Metashell does also provide a profiling feature, it is tempting to measure performance with it. This turns out to be a bad idea when comparing such performance numbers with real compiler performance: Not only are compilers significantly faster than meta shell, but they also do generate completely different numbers.

It is generally fine, that Metashell instantiates templates slower than compilers do. Metashell is meant as a development tool, and not as a high performance compiler. However, using it to compare the performance of different algorithms can result in very misleading numbers.

Metashell

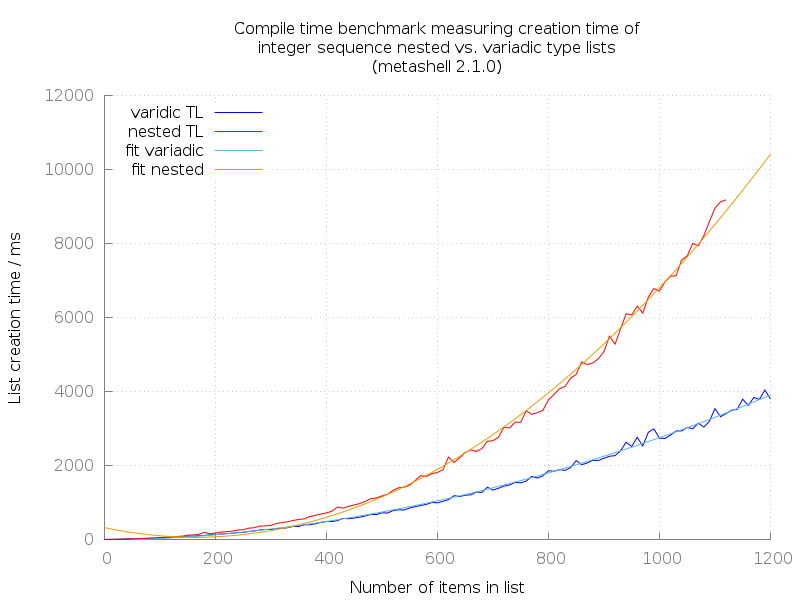
The graphs both have fitted polygonal function overlays. The runtime of generating lists, both nested and variadic types, is obviously within \(\mathcal{O}(n^2)\). This is usually something which would be considered having linear runtime, because the lists grow linearly.

These numbers turn out to be completely different when measured on real compilers like Clang and GCC:

Compilers

To my knowledge it is not possible to measure only the actual template instantiation time when using a compiler. Hence i just measured how long it takes the compiler to start, instantiate the template code, and exit again. These numbers are inherently more noisy than the metashell numbers.

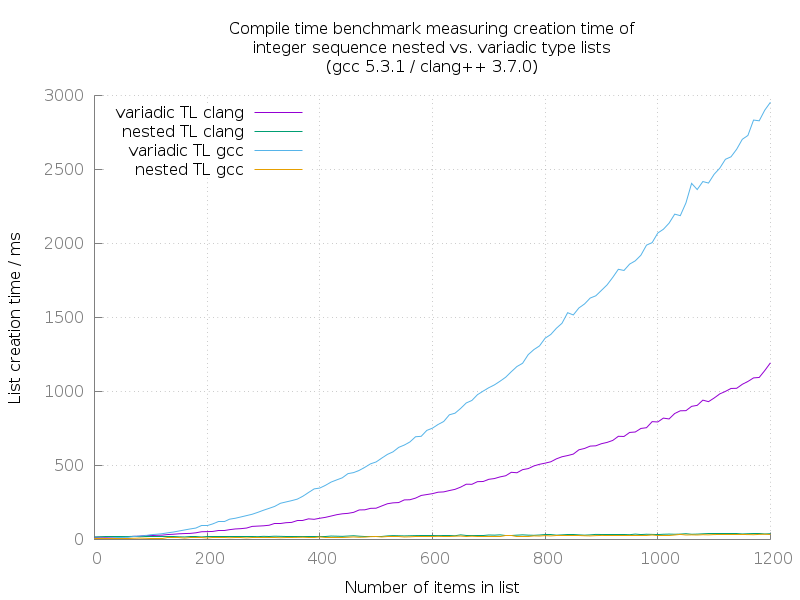
GCC/Clang: Compile time benchmark measuring creation time of integer sequence nested vs. variadic type lists

Both GCC and Clang are much faster in instantiating large variadic lists, compared to Metashell. But what is most obvious on this graph, is that nested type lists in turn are much faster than variadic type lists.

Variadic type lists are easier to read and write for programmers, but this performance penalty makes their use inpractiable for algorithms. Hence, variadic type lists can nicely be used as input/output interface to the user (the coder). But inbetween, they should be converted to type lists, in order to work efficiently on the data they convey. This article explains how to convert between different type list formats.

The performance numbers of GCC and Clang when instantiating nested type lists, look really similar in this diagram. They actually are, and i do not provide another diagram showing only these two graphs. A comparison between them based on this data would not be too fair, as these graphs are really noisy. It would be easier to compare with even larger type lists, but i experienced compiler crashes with even higher numbers.

Filtering Lists

The next thing to measure after creating lists, is applying operations on them. I chose to measure how long it takes to apply a filter on a list. The filter itself is rather cheap: I implemented functions which take a list of integer sequences, and return a list of integer sequences, but inbetween remove all even numbers.

I wrote one benchmark measuring different implementations (a code snippet appendix follows at the end of the article):

Filtering the even numbers out using the if_else_t construct
Filtering the even numbers out using pattern matching
Generating lists which do not contain even numbers from the beginning

Comparing the same algorithm using if_else_t vs. pattern matching is interesting, because there are obvious performance differences.

I tried to do a fair comparison between filtering nested and variadic type lists. To ensure this, i implemented the if-else/pattern-matching variants once in a way that the same implementation works on both kinds of lists.

All these algorithms are applied to both nested and variadic type lists. As the list creation benchmark already suggests, the nested variants of these algorithms will be faster. This time, the differences between Clang and GCC are more significant when looking at the nested variants, hence i present another diagram plotting only these.

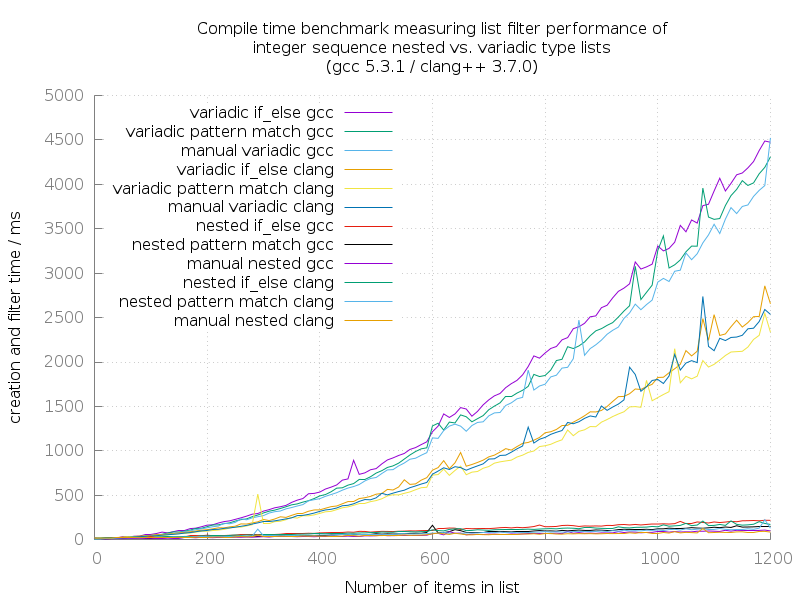
GCC/Clang: Compile time benchmark measuring list filter performance of integer sequence nested vs. variadic type lists

There are three obvious clusters in this diagram:

Variadic list operations on GCC

This cluster shows very nicely, that the performance using if_else_t for filtering items is worst, compared to all other variants. Applying pattern matching is indeed faster.

The most performant variant is assembling an already filtered list. This effectively removes the overhead of at first generating a full sequence, and filtering it afterwards.

Variadic list operations on Clang

Here, we see a generally similar pattern compared to the variadic-GCC-cluster before, but it is a bit faster with this compiler. Clang handles variadic type lists faster than GCC does.

Apart from that, the pattern matching style filter operation on the type list is faster, than creating an already filtered list. For some reason. I don’t know.

Nested list operations on Clang/GCC

All of these transformations on nested type lists are generally faster, and they are much faster.

Because the differences are not obvious on the first diagram, they are extracted and plotted on a nested-only diagram:

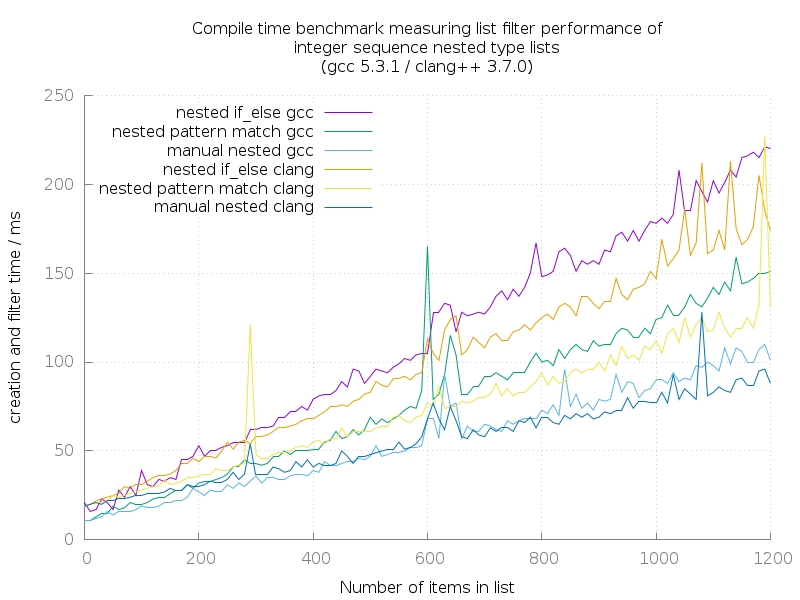
GCC/Clang: Compile time benchmark measuring list filter performance of integer sequence nested type lists

These numbers are very noisy, because they are near to the general process start time of the compiler executable in the shell.

Apart from that, the two different implementations of list filter operations, and manual filtered list creation have the same performance characteristics like before, when compared to each other.

Interestingly, clang seems to be slower for small type lists, because the time it takes to launch and return to shell is larger. For large type lists (which means they contain about 500 and more items), clang takes over and compiles faster.

The most important observation here is, that the runtime of these algorithms on nested type lists seems to be within \(\mathcal{O}(n)\). Creating variadic type lists alone is already \(\mathcal{O}(n^2)\).

The Implementations

This section shows the implementations of what i actually measured. There’s not much explanation how this works, because i wrote other articles covering that:

To understand basics like if_else_t, and pattern matching, have a look at the template meta programming basics 101 article.
To understand, how type lists work, please have a look at the type list article.

Both list filter implementations remove even numbers from the input type list. They are implemented in a way that they can handle both variadic and nested type lists.

Only for creating already filtered lists, there are two different implementations for the different types of type lists.

For all functions, at the very bottom of every example, there is an odds_t using clause, which represents the actual user interface.

if_else_t

template <typename List>
struct odds
{
    static constexpr const int  val    {head_t<List>::value};
    static constexpr const bool is_odd {(val % 2) != 0};
    using next = typename odds<tail_t<List>>::type;

    // If odd, prepend value to list. Else, skip it:
    using type = if_else_t<is_odd,
                    prepend_t<next, head_t<List>>,
                    next
                 >;
};

// Recursion terminator for nested type lists
template <>
struct odds<rec_tl::null_t>
{
    using type = rec_tl::null_t;
};

// Recursion terminator for variadic type lists
template <>
struct odds<var_tl::tl<>>
{
    using type = var_tl::tl<>;
};

template <typename List>
using odds_t = typename odds<List>::type;

Pattern Matching

// is_odd = true: Prepend item to list
// This is not a template specialization, but there is a template
// specialization afterwards, which assumes is_odd=false.
// Hence, this is an implicit specialization on is_odd=true cases.
template <bool is_odd, typename Head, typename List>
struct odds
{
    using next = typename odds<
                            (head_t<List>::value % 2) != 0,
                            head_t<List>,
                            tail_t<List>>::type;
    using type = prepend_t<next, Head>;
};

// is_odd = false: Skip item
template <typename Head, typename List>
struct odds<false, Head, List>
{
    using type = typename odds<
                            (head_t<List>::value % 2) != 0,
                            head_t<List>,
                            tail_t<List>>::type;
};

// Recursion terminator for nested type lists
// Last element: is_odd = true
template <typename Head>
struct odds<true, Head, rec_tl::null_t>
{
    using type = rec_tl::tl<Head, rec_tl::null_t>;
};

// Recursion terminator for nested type lists
// Last element: is_odd = false
template <typename Head>
struct odds<false, Head, rec_tl::null_t>
{
    using type = rec_tl::null_t;
};

// Recursion terminator for variadic type lists
// Last element: is_odd = true
template <typename Head>
struct odds<true, Head, var_tl::tl<>>
{
    using type = var_tl::tl<Head>;
};

// Recursion terminator for variadic type lists
// Last element: is_odd = false
template <typename Head>
struct odds<false, Head, var_tl::tl<>>
{
    using type = var_tl::tl<>;
};

template <typename List>
using odds_t = typename odds<
                            (head_t<List>::value % 2) != 0,
                            head_t<List>,
                            tail_t<List>>::type;

Filtered List Generation

Nested:

template <bool is_odd, typename Head, typename List>
struct odds;

template <typename Head, typename TailHead, typename TailTail>
struct odds<true, Head, rec_tl::tl<TailHead, TailTail>>
{
    using next = typename odds<
                            (TailHead::value % 2) != 0,
                            TailHead,
                            TailTail>::type;
    using type = rec_tl::tl<Head, next>
};

template <typename Head, typename TailHead, typename TailTail>
struct odds<false, Head, rec_tl::tl<TailHead, TailTail>>
{
    using type = typename odds<
                            (TailHead::value % 2) != 0,
                            TailHead,
                            TailTail>::type;
};

template <typename Head>
struct odds<true, Head, rec_tl::null_t>
{
    using type = rec_tl::tl<Head, rec_tl::null_t>;
};

template <typename Head>
struct odds<false, Head, rec_tl::null_t>
{
    using type = rec_tl::null_t;
};

template <typename List>
using odds_t = typename odds<
                            (head_t<List>::value % 2) != 0,
                            head_t<List>,
                            tail_t<List>>::type;

Variadic:

template <bool is_odd, typename Current, typename InList, typename OutList>
struct odds;

template <typename Current, typename InHead,
          typename ... InTail, typename ... Outs>
struct odds<true, Current, var_tl::tl<InHead, InTail...>, var_tl::tl<Outs...>>
{
    using type = typename odds<
                            (InHead::value % 2) != 0,
                            InHead,
                            var_tl::tl<InTail...>,
                            var_tl::tl<Outs..., Current>>::type;
};

template <typename Current, typename InHead,
          typename ... InTail, typename ... Outs>
struct odds<false, Current, var_tl::tl<InHead, InTail...>, var_tl::tl<Outs...>>
{
    using type = typename odds<
                            (InHead::value % 2) != 0,
                            InHead,
                            var_tl::tl<InTail...>,
                            var_tl::tl<Outs...>>::type;
};

template <typename Current, typename ... Outs>
struct odds<true, Current, var_tl::tl<>, var_tl::tl<Outs...>>
{
    using type = var_tl::tl<Outs..., Current>;
};

template <typename Current, typename ... Outs>
struct odds<false, Current, var_tl::tl<>, var_tl::tl<Outs...>>
{
    using type = var_tl::tl<Outs...>;
};

template <typename List>
using odds_t = typename odds<
                        (head_t<List>::value % 2) != 0,
                        head_t<List>,
                        tail_t<List>,
                        var_tl::tl<>>::type;

Conclusion

What i learned from my previous C++ TMP experience, and these benchmarks;

Branching using pattern matching is generally faster than if_else_t
Modifying nested type lists is generally faster than variadic type lists.
Metashell is fine for debugging C++ TMP code, but not for actual measuring

I hope these insights are also useful for others!

Type List Compile Time Performance