What does the math tell us about how many job applicants we should look at before hiring one? While onboarding our new employees, how can ideas from the TCP networking protocol help us to identify the optimal workload for them? Why would giving employees unlimited vacation days most likely lead to less vacation being taken? Algorithms to live By - The Computer Science of Human Decisions gives some fascinating insights into such questions.

Book & Authors
The first edition of this book is from 2016 and the store page on Amazon says that since 2017 it’s already the 12th edition. It is ~370 pages in total but the actual content without notes etc. is just about 260 pages.
Brian Christian is a non-fiction author, speaker, poet, programmer (e.g. Ruby on Rails contributor), and researcher. This book and his other books, The Most Human Human and The Alignment Problem won several awards.
Tom Griffiths is a professor of computer science and psychology and the director of the Computational Cognitive Science Lab at Princeton University.
Content and Structure
The authors selected 11 topics from mathematics and computer science. In each chapter, they describe practical and relevant challenges from real life that can be solved with formulas and algorithms. If you ever asked yourself “What’s the point? I will never use this in real life!” at school or university, these are for you!
The authors spend some time explaining probabilities, trade-offs, complexities, etc. with scientific methods, but they don’t go too deep. This makes the content comprehensible for nearly everyone, especially interested readers who never studied anything mathematical/technical. I might not be the best person to judge that because I did study at university, but I am certain that as long as seeing variable names or diagrams does not straightly trigger fear, you should be able to understand it and experience fun reading the stories.
Let’s get to the different chapters and their content. This review is much longer than the others in my blog: The different chapters provide valuable insights, but on mostly disconnected topics. I did not want to drop any.
1. Optimal Stopping - When to Stop Looking
This chapter is about the stopping problem, which is a classic decision-making problem that involves choosing the optimal time to stop a process or activity. When you want to find the best specimen out of an unknown set (in the sense that you don’t know what’s the lower and upper bounds of “good” are), the Look-Then-Leap rule states that you should set an amount of time you want to spend looking. This amount of time should then be split into a looking phase and a leaping phase. In the looking phase, you categorically don’t choose anyone. After that point, you enter the leaping phase and commit to the next candidate who outshines the best applicants from the looking phase. The looking phase shall occupy 37% of the time or the number of candidates you can afford to look at. This leads to a 37% chance of selecting the best (That it’s both 37% is a coincidence that results from the maths). 37% does not appear great, but is better or worse than the gut feeling?

This strategy can be used in a variety of interesting situations:
- The Secretary Problem: Choosing the best candidate from a pool of applicants
- Selling a house: Determining the best offer
- Finding a partner: Deciding when to commit to a relationship after a series of different dates
- Selecting a parking lot: Choosing the best parking space available while trading off between how far it is from your flat and how often you will have to do another round around the block
- Quitting an activity: Deciding when to stop doing something
2. Explore/Exploit - The Latest vs. the Greatest
This chapter starts with the very concrete question of when you should stick to the restaurants you know to be good, and when to try out new ones. It turns out that this is the same problem that casino visitors face in a saloon full of one-armed bandits: Should they try the same bandit again, or should they switch to another one? It’s also the same problem that marketing specialists face when they do A/B testing of different wordings or styles of advertisements (the book mentions that Google tested 41 shades of blue for a toolbar in 2009).

The Gittins Index models a strategy for deciding when to switch from one solution to another, based on the history of success rates. The way it works is that each alternative gets a score. For every decision, the alternative with the highest score is selected. Based on success or failure, the score is updated following a specific scheme. This strategy results in the following behavior:
- Untested options are tried if the tested ones go below a success rate of 70%
- The strategy is more merciful on failing alternatives in the beginning than on long-known alternatives
Switching or not switching between alternatives raises questions about other use cases: In clinical studies, the set of voluntary patients (or not so voluntary if the only cure is still experimental) is split into a group that gets the new experimental medicine, and another group that gets placebos. When the study is only half over but the new treatment already proved very effective, how ethical is it to stick to giving the placebo group placebos instead of switching over all patients to the seemingly effective treatment? Switching might however jeopardize the needed statistical backing that is needed to approve the effectiveness of new treatments.
While the Gittins Index looks at the past, the chapter also introduces the reader to other strategies as the regret minimization strategy based on so-called Upper Confidence Bound algorithms, which take assumptions on the future into account. These give the benefit of the doubt a mathematical backing:
Following the advice of these algorithms, you should be excited to meet new people and try new things — to assume the best about them, in the absence of evidence to the contrary. In the long run, optimism is the best prevention for regret.
When looking at the future, it also becomes relevant how much time is left:
Explore when you will have time to use the resulting knowledge and exploit when you’re ready to cash in. The interval makes the strategy.
3. Sorting - Making Order
This chapter handles sorting theory and discusses the cost of sorting. Sorting costs time (and comparisons - sometimes these are not free), which is something that computer science students learn to quantify with complexity theory up and down, typically by analyzing different sorting algorithms and estimating their costs as a function of the input size.

Ever thought about how long it would take to sort a deck of 5 cards? Or 10? Or 20? The cost of sorting them goes up much steeper than the deck of cards grows. The book demonstrates the science behind scale nicely to non-computer-scientists using more examples that show how much scale hurts when sorting inputs that are just too big. Social hierarchies and pecking orders have been established with physical fighting as sorting methods, which puts the “cost” of comparison/sorting in a completely different perspective. Civilization has brought softer and more efficient ways to sort with sports and markets, which resemble crowd algorithms, so to say.
The example of sports is explained more in-depth: Championships and leagues are a way to sort teams by performance. For sports where one person or team competes version one other at a time, complex tournament strategies like Single Elimination, Round Robin, Ladder, and Bracket Tournament strategies are used. Races with many competitors are simpler, but even these have qualifying events, which sort them before the race which is supposed to sort them in the first place. Each of these strategies resembles different sort algorithms for different problem sizes, long before sorting algorithms have been formalized.
Even search machines offer some kind of sorting, although this is surprising at first: You enter some search words into Google, and Google presents you not one but many websites - sorted by relevance.
4. Caching - Forget About It
This chapter motivates the concept of “caching” by explaining memory hierarchies: Computers have smaller portions of very fast but expensive memory and bigger portions of memory that is cheap but slow. Users like their computers fast, so engineers have to deal with the challenge to provide the right data at the right time from limited faster memory.

Phil Karlton, at that time an engineer at Carnegie Mellon, half-jokingly originated this quote around 1970:
There are only two hard things in Computer Science: Cache invalidation and naming things.
The chapter before was all about sorting data to make specific items easier to find. This chapter brings some (half-joking) news for the lazy. With all the knowledge about caching, it turns out, that not sorting data can shorten access times a lot:
Tom’s otherwise extremely tolerant wife objects to a pile of clothes next to the bed, despite his insistence that it’s in fact a highly efficient caching scheme. Fortunately, our conversations with computer scientists revealed a solution to this problem too. Rik Belew of UC San Diego, who studies search engines from a cognitive perspective, recommended the use of a valet stand.
The mentioned “pile of clothes” in some sense resembles the Least Recently Used caching scheme:
LRU teaches us that the next thing we can expect to need is the last one we needed, while the thing we’ll need after that is probably the second-most-recent one. And the last thing we can expect to need is the one we’ve already gone the longest without.
The chapter makes interesting detours between principles known from computer science like Beladys Anomaly, First-In-First-Out (FIFO), and Random Replacement, and shows how similar these principles are to processes that happen in our brains, like the Human Forgetting Curve, which is a known phenomenon from neurosciences and psychology.
The science of caching can not only be applied to computers, but also the physical layout of library rooms, the ordering of clothes in the bedroom, management of post-its, and shelves, and why/when/how people remember or forget things:
Caching gives us the language to understand what’s happening. We say “brain fart” when we should really say “cache miss”.
5. Scheduling - First Things First
Beginning with the question of how to schedule tasks in everyday life, the book delves briefly into how computers schedule technical tasks, and what to learn from them:
The first lesson in single-machine scheduling is literally before we even begin: make your goals explicit.
As things are generally a bit more arranged in computer memory than in real life, it is easier to summarize observations and extract guidelines:
Minimizing the sum of completion times leads to a very simple optimal algorithm called Shortest Processing Time: Always do the quickest task you can.

After a few motivating examples that relate to real-life tasks, the amount of theory is ramped up a bit, for example when explaining Earliest Due Date (also called Moore’s Algorithm) vs Shortest Processing Time and discussing such strategies with real-life problems (e.g. something bad happens when a deadline is crossed).
This example cracked me up:
There’s an episode of The X-Files where the protagonist Mulder, bedridden and about to be consumed by an obsessive-compulsive vampire, spills a bag of sunflower seeds on the floor in self-defense. The vampire, powerless against his compulsion, stoops to pick them up one by one, and ultimately the sun rises before he can make a meal of Mulder. Computer scientists would call this a “ping attack” or a “denial of service” attack: Give a system an overwhelming number of trivial things to do, and the important things get lost in the chaos.
The chapter also goes a meta-level up: A perfect schedule or time plan must reflect two things:
[…], preemption isn’t free. Every time you switch tasks, you pay a price, known in computer science as a context switch.
The little pause between two tasks should be reflected, otherwise, we drown in task switching:
Anyone you interrupt more than a few times an hour is in danger of doing no work at all.
…for which computer science also has a name: Thrashing Phenomenon
But that is not all, the time in which we are rethinking to create the plan must also be part of the plan, which is where it gets complicated. In many cases, no perfect plan exists because whenever a human or a machine waits for external events to happen, they have to deal with uncertainty and in between do what’s possible, which in turn brings new problems:
What makes real-time scheduling so complex and interesting is that it is fundamentally a negotiation between two principles that aren’t fully compatible. These two principles are called responsiveness and throughput: How quickly you can respond to things, and how much you can get done overall.
Most computer scientists already know this example from real-time scheduling lectures at university, but I think that this is one of the most interesting examples in this chapter:
For the first time ever, a rover was navigating the surface of Mars. The $150 million Mars Pathfinder spacecraft had accelerated to a speed of 16,000 miles per hour, traveled across 309 million miles of empty space and landed with space-grade airbags onto the rocky red Martian surface. And now it was procrastinating.
By procrastinating the author means that the $150 million Pathfinder was not responding to commands from the earth due to a scheduling problem called Priority Inversion. A good solution for priority inversion is Priority Inheritance: If you realize that employees come late to very important meetings all the time, do some research to find the reason and find out that the coffee machine is so slow that employees end up in endless queues: Increase the importance of high-quality coffee machine maintenance to the same level like the most important meetings.
The main message is:
As business writer and coder Jason Fried says, “Feel like you can’t proceed until you have a bulletproof plan in place? Replace ‘plan’ with ‘guess’ and take it easy.” Scheduling theory bears this out.
6. Bayes’s Rule - Predicting the Future
This chapter begins with a problem that, if it was solved, would make scheduling much easier: Predicting the future. Statistics and stochastic theory are typically used to model the certainty of the timing and quantity of events or things. The whole chapter starts with historic developments on this matter and tries to make it entertaining a bit, but statistics are still notoriously hard to make look interesting.
The biggest part of the chapter educates (in easy-to-understand ways) about Bayes’ Rule, Laplace’s Law, the Copernican Principle, normal distribution vs. power-law distribution, and many others, which is relatively boring. After we read through that part (or skipped it), we reach my favorite example:

The Marshmallow experiment is widely known:
Each child would be shown a delicious treat, such as a marshmallow, and told that the adult running the experiment was about to leave the room for a while. If they wanted to, they could eat the treat right away. But if they waited until the experimenter came back, they would get two treats. Unable to resist, some of the children ate the treat immediately. And some of them stuck it out for the full fifteen minutes or so until the experimenter returned, and got two treats as promised.
Everyone who knows about this experiment also knows that long-time observation of these kids suggested that the ones who are patient enough to wait to get both marshmallows are also generally more successful in their later life (which has to be questioned because the study has been repeated to find out that the statistical significance is too weak). The chapter however continues with an interesting twist, which is by far not as widely known:
[…] the most interesting group comprised the ones in between — the ones who managed to wait a little while, but then surrendered and ate the treat.
The researchers tried to find out why kids would behave so irrationally - is it a sheer lack of discipline? They found out that it is more about trust in authorities than discipline:
[…], the kids in the experiment embarked on an art project. The experimenter gave them some mediocre supplies and promised to be back with better options soon. But, unbeknownst to them, the children were divided into two groups. In one group, the experimenter was reliable and came back with the better art supplies as promised. In the other, she was unreliable, coming back with nothing but apologies.
When the marshmallow experiment was repeated with children who first went through this experiment, the results showed that the children which were disappointed by the experimenter would more likely give up in the middle of the marshmallow experiment. I thought about this a little longer - This is an interesting data point for potential disadvantages that many (poor/less successful) people might suffer from: Some may have grown up in environments where they have been disappointed by their parents/authorities too often and ended up trusting less in such investments.
7. Overfitting - When to Think Less
This chapter was very interesting and captivating read: The phenomenon of overfitting is a known problem in the domain of artificial intelligence/machine learning. Most explanations are extremely abstract and hard to grasp for outsiders. But actually, overfitting is very easy to understand when explained through real-life situations:
In the military and in law enforcement, for example, repetitive, rote training is considered a key means for instilling line-of-fire skills. The goal is to drill certain motions and tactics to the point that they become totally automatic. But when overfitting creeps in, it can prove disastrous. There are stories of police officers who find themselves, for instance, taking time out during a gunfight to put their spent casings in their pockets — good etiquette on a firing range.

The effect of this case of overfitting was an unnecessary increase in dead officers:
On several occasions, dead cops were found with brass in their hands, dying in the middle of an administrative procedure that had been drilled into them.
Another example from the same domain goes like this:
[…] the FBI was forced to change its training after agents were found reflexively firing two shots and then holstering their weapon—a standard cadence in training — regardless of whether their shots had hit the target and whether there was still a threat. Mistakes like these are known in law enforcement and the military as “training scars,” and they reflect the fact that it’s possible to overfit one’s own preparation.
Overfitting and the difficulty to set incentives in a way that they don’t end up being counter-effective have a lot of overlap:
[…] focusing on production metrics led supervisors to neglect maintenance and repairs, setting up future catastrophe. Such problems can’t simply be dismissed as a failure to achieve management goals. Rather, they are the opposite: The ruthless and clever optimization of the wrong thing.
The presented examples were my highlights, but the chapter has some more good ones. Out of all the theory and real-life examples, the authors extract one piece of good advice against overthinking:
The greater the uncertainty, the bigger the gap between what you can measure and what matters, the more you should watch out for overfitting — that is, the more you should prefer simplicity, and the earlier you should stop.
8. Relaxation - Let It Slide
At university in group assignments, but also later at work while discussing with colleagues, I often experienced that perfect is the enemy of the good: The group of students or colleagues would rather discuss forever while ditching one 80-90% idea after the other, instead of simply deciding for one and live with a “good” result. (After having the last chapter also discussing the difficulty of setting good incentives: Often company culture makes employees want to avoid making mistakes to not damage their career, so it seems better to discuss perfect solutions forever.)

This is irrational, but what’s the rational way if a problem looks too hard to solve? In computer science, problems are considered “too hard” when the runtime and/or memory complexity of finding the solution has exponential growth (instead of polynomial, which is considered “easy”). The chapter contains strategies and algorithms that do Constraint Relaxation:
But [computer scientists] don’t relax themselves; they relax the problem.
The first example that can be solved faster with this strategy is the Traveling Salesman Problem: If you want to visit many places, what is the right order to visit them that at the same time gives you the shortest overall travel distance? To really find out, one would have to sum up the travel distances of all possible paths and then take the shortest one out of the huge list. Constraint relaxing algorithms make shortcuts and are hence faster, but don’t guarantee you the correct result - instead, you get a “good” answer that’s most probably better than following your gut feeling or just trying randomly. The message is clear:
If we’re willing to accept solutions that are close enough, then even some of the hairiest problems around can be tamed with the right techniques.
This chapter is really short and less technical than the following ones which will pick up on relaxation again, but it leaves another very interesting life-philosophic inspiration:
One day as a child, Brian was complaining to his mother about all the things he had to do: his homework, his chores… “Technically, you don’t have to do anything,” his mother replied. “You don’t have to do what your teachers tell you. You don’t have to do what I tell you. You don’t even have to obey the law. There are consequences to everything, and you get to decide whether you want to face those consequences.” Brian’s kid-mind was blown. It was a powerful message, an awakening of a sense of agency, responsibility, moral judgment.
It was probably not clear to both at that moment, but she taught him Lagrangian Relaxation: Take rules (constraints) and transform them into costs which means taking the impossible and downgrading it to costly. Sometimes the consequences of breaking some rules are less bad than not solving some bigger problem.
9. Randomness - When to Leave It to Chance
We usually only leave important things to chance (if at all) when we exhausted all other strategies, and they did not work out. This chapter illuminates some use cases where introducing randomness into algorithms makes them perform better than deterministic algorithms would. Again, let us skip over the rich details and background stories that are shared about the Monte Carlo Method, Bloom Filters, Hill Climbing, Metropolis Algorithm, and Simulated Annealing. Instead, let’s have a look at the Miller-Rabin Primality Test and its significance to the majority of private communication on this planet:
When encrypting messages before sending and decrypting after receiving them,
we typically rely on
asymmetric cryptography.
For the user, this means that encryption and decryption are done with different
keys.
Having different keys has the advantage that the key for encryption can be
publicly shared, enabling anyone to send us an encrypted message that only we
can read.
The decryption key is stored and protected in private.
Without going too deep into detail, such algorithms rely on the fact that there
are no “fast” (following the notion of fast from the earlier chapters)
mathematical algorithms that can reverse multiplication or exponentiation of
very large numbers if not all variables are known (i.e. the key that is part of
the calculation).
A simple example with small numbers is the question “What are the two prime
factors of the number 15?”.
The answer is: 3 * 5 equals 15 as both 3 and 5 are prime and there
is no other combination of prime numbers for which this works, so this
is the correct answer.
For small numbers, this is very easy, but for huge numbers, computers would need
centuries - so the designers of algorithms like
PGP decided to rely on the
security of messages on this fact:
The user’s private key for decryption consists of two huge prime numbers and
must be kept secret.
The public key that the user can freely send around consists of … the
product of these numbers. (So if the combination of 3 and 5 would be the
user’s private key, the product 15 would be the public one!)
This means that everyone actually has access to the secret private key.
It is nonetheless safe from being misused because no one can extract the
two individual prime numbers from it.
This might sound like a wonky foundation for security for everyone who thought
that messages are only secure if third parties cannot decrypt
them, but such a perfect algorithm does not exist:
The best we can get is that it’s only too hard to decrypt a message within the
same century.
It does not stop there:
Let’s see how the user selects the prime numbers.
When running a mail program or secure messenger for the first time, the laptop
or cell phone would automatically generate a key for the user
(Often hidden from the user’s sight to improve the user experience).
To get two huge prime numbers, the program rolls the dice to get
two huge numbers and then tests if they are prime.
If they are not, it rolls the dice again and again, until it has two huge prime
numbers.
Testing if a number is a prime number is typically done with the
Miller-Rabin Primality Test.
This test consists of a formula that is cheap to compute.
Its result tells if the number is a strong probable prime or not - it can’t
say if it is a prime, but only if it is likely one.
To get to 99.999999...% (and many more nines) probability of being
correct, the algorithm is repeated a lot.
Now we (or our messenger application) know that we have two prime numbers that
are most probably prime, and unlikely to have been chosen by someone else for
their keys, so we can now happily encrypt our most secret and important
messages with them.
This might again sound like a wonky foundation, but it’s more probable to end up
with insecure keys due to
broken random number generators
than due to trusting the probabilities from the encryption algorithms.
I learned about these things at university in multiple cryptography lectures,
but we were too busy learning how they work to have a look at the history
and real-life stories, so reading about it again from some fresh perspective in
this book was enlightening.
The main message of this chapter is:
There is a deep message in the fact that on certain problems, randomized approaches can outperform even the best deterministic ones. Sometimes the best solution to a problem is to turn to chance rather than trying to fully reason out an answer.
10. Networking - How We Connect
After beginning with a historic tour of the content of the first telegraph, first phone call, first mobile phone call, and first text message over the internet, the first subsection finds an elegant conclusion:
The foundation of human connection is protocol — a shared convention of procedures and expectations, from handshakes and hellos to etiquette, politesse, and the full gamut of social norms. Machine connection is no different. Protocol is how we get on the same page; in fact, the word is rooted in the Greek protokollon, “first glue,” which referred to the outer page attached to a book or manuscript.
Most of the chapter goes into explaining how switched packet networking works because all the digital communication on the planet relies on it. The interesting bit of switched networking is that there is no such thing as a connection like telephone calls used to have, although video meeting apps tell you the opposite. Ditching dedicated connections gives more flexibility because computers don’t maintain only a few connections that are used all the time, but instead maintain many connections which are only used in bursts. The book shares the amount of technical detail about TCP, Congestion Control, the Byzantine Generals Problem, and Exponential Backoff that is needed to bridge the ideas behind them with real-life scenarios that most readers know.

I liked how the authors found something in nature that makes TCP’s flow control strategy look very natural:
Other animal behavior also evokes TCP flow control, with its characteristic sawtooth. Squirrels and pigeons going after human food scraps will creep forward a step at a time, occasionally leap back, then steadily creep forward again.
This strategy is also called Additive Increase/Multiplicative Decrease due to its nature to increment the send rate in small steps while the transmission of packets is successful but drop the rate drastically in case of transmission errors. This way messages are often sent at a slower rate than possible, but transmission errors are kept to a minimum.
The book suggests the application of the AIMD strategy during the onboarding of new employees: If it’s unclear how much they will perform in their new environment, increase their workload in small steps, and as soon as they appear overloaded and make too many mistakes due to stress, drastically reduce the number again. Midterm, the employee would work slightly below their maximum and not be over-stressed, which is good for all participants.
Application of this strategy would also have a positive long-term impact if applied as a countermeasure against the bad effects of the Peter principle: Employees are promoted based on their success in previous jobs until they reach a level at which they are no longer competent, as skills in one job do not necessarily translate to another. The AIMD strategy suggests that we should be able to demote people again if their last promotion decreased the overall organization’s strength (it does not appear useful in this case to demote the person multiple levels lower although AIMD works like that, depending on the metrics).
Two other interesting messages can be extracted from this chapter:
In 2014, for instance, UC Santa Cruz’s Jackson Tolins and Jean Fox Tree demonstrated that those inconspicuous “uh-huhs” and “yeahs” and “hmms” and “ohs” that pepper our speech perform distinct, precise roles in regulating the flow of information from speaker to listener—both its rate and level of detail. Indeed, they are every bit as critical as ACKs are in TCP. Says Tolins, “Really, while some people may be worse than others, ‘bad storytellers’ can at least partly blame their audience.”
I liked to read this because it backs something that I always felt in online meetings: If all or most participants are on mute with disabled webcams, it hurts the effectiveness of online meetings. Unfortunately, I have seen this online meeting culture a lot. I typically also annoy the students of my university lecture into enabling their webcams because it enables me to present them with a better listening experience when I see the students’ faces: If they look annoyed, I might have been talking about the same thing for too long (thinking that the majority does not understand it yet) and if they pinch their eyes, I might have skipped over something too quickly. Giving some kind of talk in front of a screen without faces on it is a bad experience and makes it harder to give the audience a good experience.
My last highlight of this chapter is the explanation of the technical phenomenon in computer networks called Buffer Bloat: When network devices that are under heavy load are configured with too large buffers (This is typically not a configuration knob that is visible for end-users) to queue up packets that can’t be processed yet, then this often impacts latencies of TCP network connections negatively. The real-life example that the authors came up with to explain this to non-engineers is strikingly simple:
When Tom took his daughter to a Cinco de Mayo festival in Berkeley, she set her heart on a chocolate banana crêpe, so they got in line and waited. Eventually — after twenty minutes — Tom got to the front of the line and placed his order. But after paying, they then had to wait forty more minutes to actually get the crêpe.
The solution for this problem is simple and works both on network devices and in crêpe shops:
Turning customers away would have made everyone better off—whether they ended up in a shorter crêpe line or went elsewhere. And wouldn’t have cost the crêpe stand a dime of lost sales, because either way they can only sell as many crêpes as they can make in a day, regardless of how long their customers are waiting.
This might suggest finding peace with one or the other dropped packet, and more generally in life learning to say “no”: If you tend to accept too many requests from others to not disappoint them, you will end up disappointing them with long wait times anyway.
11. Game Theory - The Minds of Others
Game Theory is all about studying the rules of games and the strategies that players can follow to get the best results for them. This chapter explains the so-called Nash Equilibrium, which is a state of any game where all players found the strategy that gives them the best result from their perspective and everyone sticks to theirs. Depending on the design of the game, this means anything between good and bad results for all players.
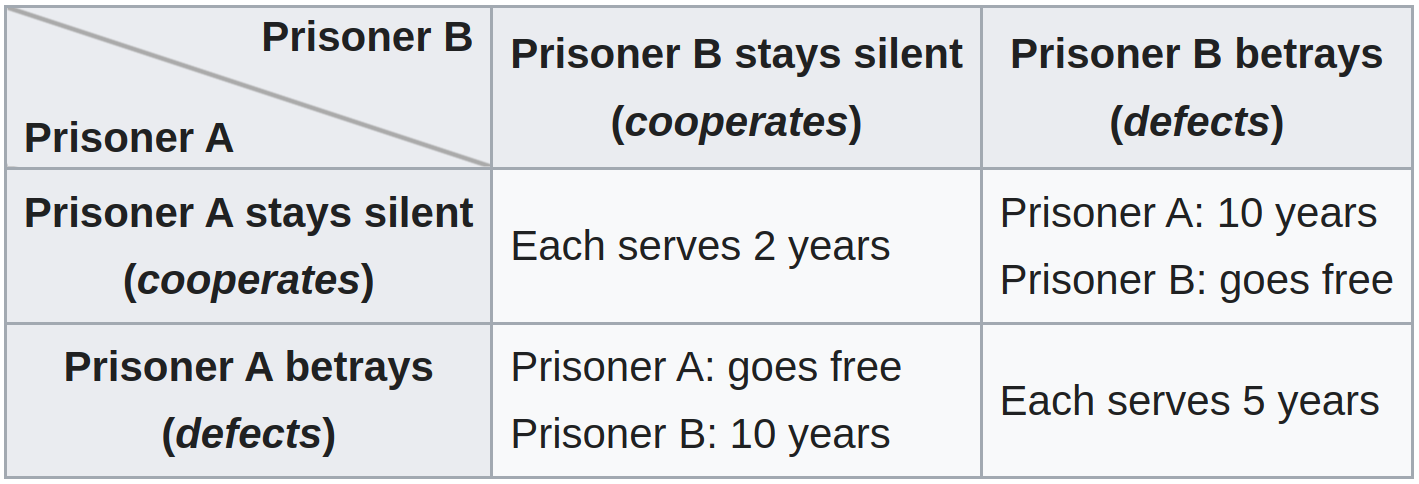
The best example of a nash equilibrium that brings bad results for the players is the Prisoner’s Dilemma: Imagine two collaborators of a crime are caught but the police do not have enough evidence to convict them on the principal charge. During the interrogation, each collaborator has the choice to remain silent or cooperate with the police, which means betraying their collaborator but getting out of jail immediately. If both collaborators betray each other they will however both end up in jail for long.
The only good way out of this game for both participants is if they really can trust each other, but the individual player will get the best “score” for them if they do the betrayal (going out of jail is still better than sitting for just a few years). The message of the prisoner’s dilemma is that if you set up a game like this, the mainstream of participants will converge on the bad behavior because this is the rational choice resulting from understanding the game. At this point, it’s easy to blame the players, but the book suggests blaming the game author for setting up the rules like this in the first place.
While the prisoner’s dilemma will most likely be familiar to most readers already, the book comes up with two other nice and intriguing examples:
Imagine two shopkeepers in a small town. Each of them can choose either to stay open seven days a week or to be open only six days a week, taking Sunday off to relax with their friends and family. If both of them take a day off, they’ll retain their existing market share and experience less stress. However, if one shopkeeper decides to open his shop seven days a week, he’ll draw extra customers
The Nash equilibrium of this game is a market where all shops are under pressure to have open all the time. Depending on the question if this is a good thing for all participants, it might be necessary to change the rules to relieve the players from pressure.
As intuitive as the market example is, the next example seems counter-intuitive and surprising at first glance. What would happen, if a company gave every one of their employees unlimited vacation time?
All employees want, in theory, to take as much vacation as possible. But they also all want to take just slightly less vacation than each other, to be perceived as more loyal, more committed, and more dedicated (hence more promotion-worthy). Everyone looks to the others for a baseline, and will take just slightly less than that. The Nash equilibrium of this game is zero.
This is shocking because it shows how quickly bad scores can result from initially well-intended rules. The authors call this the Tragedy of the Commons. Stock markets close at defined times as otherwise traders would lose money if they went to bed, leading to many burned-out traders.
Mechanism Design is then presented as the solution: Game theory asks what behavior will result from a given set of rules and mechanism design asks what set of rules should be given for the desired behavior. Mechanism design can help make the game moves that would otherwise be irrational, rational. Revenge, for example, is a very natural behavior in animals and humans, but it is irrational because it just increases the damage and does not bring anything back to anyone. Still, it seems to be helpful, because the sheer likelihood that someone would take vengeance if someone else did them badly models a counterincentive.

The next interesting principle from game theory research is the price of anarchy, which measures how much worse the average outcome of a game gets for everyone due to selfish behavior. Games with a high price of anarchy are hence worthy of being redesigned to reduce the effect of the tragedy of the commons. Calculating the price of anarchy can even show that some games don’t necessarily need a redesign, although one would intuitively think so: The price of anarchy shows that human traffic with egoistic drivers is only 33% worse than a perfect centrally planned traffic of computer drivers (not including the reduced number of accidents with injuries/deaths). There are arguments against individual car traffic, but they originate more from the scaling perspective than from game theory.
Conclusion - Computational Kindness
My favorite main message of this concluding chapter is, that mathematics and algorithms show us that we can stop stressing ourselves over always improving in all areas, because even with optimal strategies, the results are not always optimal, and accepting that is just rational. This does not mean that one should not try if science says that the probability of success is too low - but that one should try and simply adjust their expectations.

This chapter also cultivates the principle of being “computationally kind” to others:
We can be “computationally kind” to others by framing issues in terms that make the underlying computational problem easier. This matters because many problems—especially social ones, as we’ve seen—are intrinsically and inextricably hard. […] Politely withholding your preferences puts the computational problem of inferring them on the rest of the group. In contrast, politely asserting your preferences (“Personally, I’m inclined toward x. What do you think?”) helps shoulder the cognitive load of moving the group toward resolution.
Life is complicated and full of decisions with no upfront clear outcome, so relax and follow the final advice:
In the hard cases, the best algorithms are all about doing what makes the most sense in the least amount of time, which by no means involves giving careful consideration to every factor and pursuing every computation to the end. Life is just too complicated for that.
Summary
I think that the people who profit most from reading this book are curious non-technical people, people who work with (software) engineers (e.g. their managers), and early students: The examples and anecdotes are interesting and vivid, as they back otherwise boring theory with relevant and partly entertaining real-life scenarios that have strong potential to motivate further study. Computer scientists will appreciate the examples and anecdotes because they are entertaining, but also because they help to explain tricky technical situations to non-technical colleagues with good comparisons when it matters.
While reading about algorithms and strategies and their application to social situations, I remembered many situations at work where the whole team rendered trapped in escaping local maximums because solutions worked “well enough” to not change them, although there were problems that could have been solved by shaking everything up a little (as suggested by e.g. the simulated annealing algorithm). These were situations where people would use all their engineering skills to solve technical challenges, but would not use the same knowledge to challenge their feelings and comfort zone - but that is the game changer that would help many to be more innovative. A good part of the messages in this book converges to “stop overthinking, even science says that it’s more rational to try something new”.
This book is a bridge between the technical and the non-technical worlds. It is not a must-read but a very good book for everyone who likes a mixture of slight entertainment, story-telling, and a closer but not too technical look at interdisciplinary connections of life with mathematics and computer science. If you don’t read it, you might be missing out on some of the most interesting details of the inner workings of the modern world.